NBA Free Throw Modeling

A hierarchical binomial model of 2025-26 free throw shooting

I’ve been away so long, I wanted to take it back to basics. The first post we ever had was about free throw shooting, and we didn’t even use a hierarchical model. So, let’s go back to that, but we’ll start with a hierarchical model.

As usual, this is just a starting point, and in follow up posts, we’ll add more complexity as we go.

The Model

We’ll use a simple binomial hierarchical model (full model below). Where each player’s free throw ability is estimated from a league-wide distribution where the mean and variance of the league-wide distribution are learned from the data.

Importantly, if a player has only taken a handful of shots this season, the model assumes that they are basically just an average player. So naturally, we don’t need to do those arbitrary things like only limiting it to players with at least 50 free throw attempts.

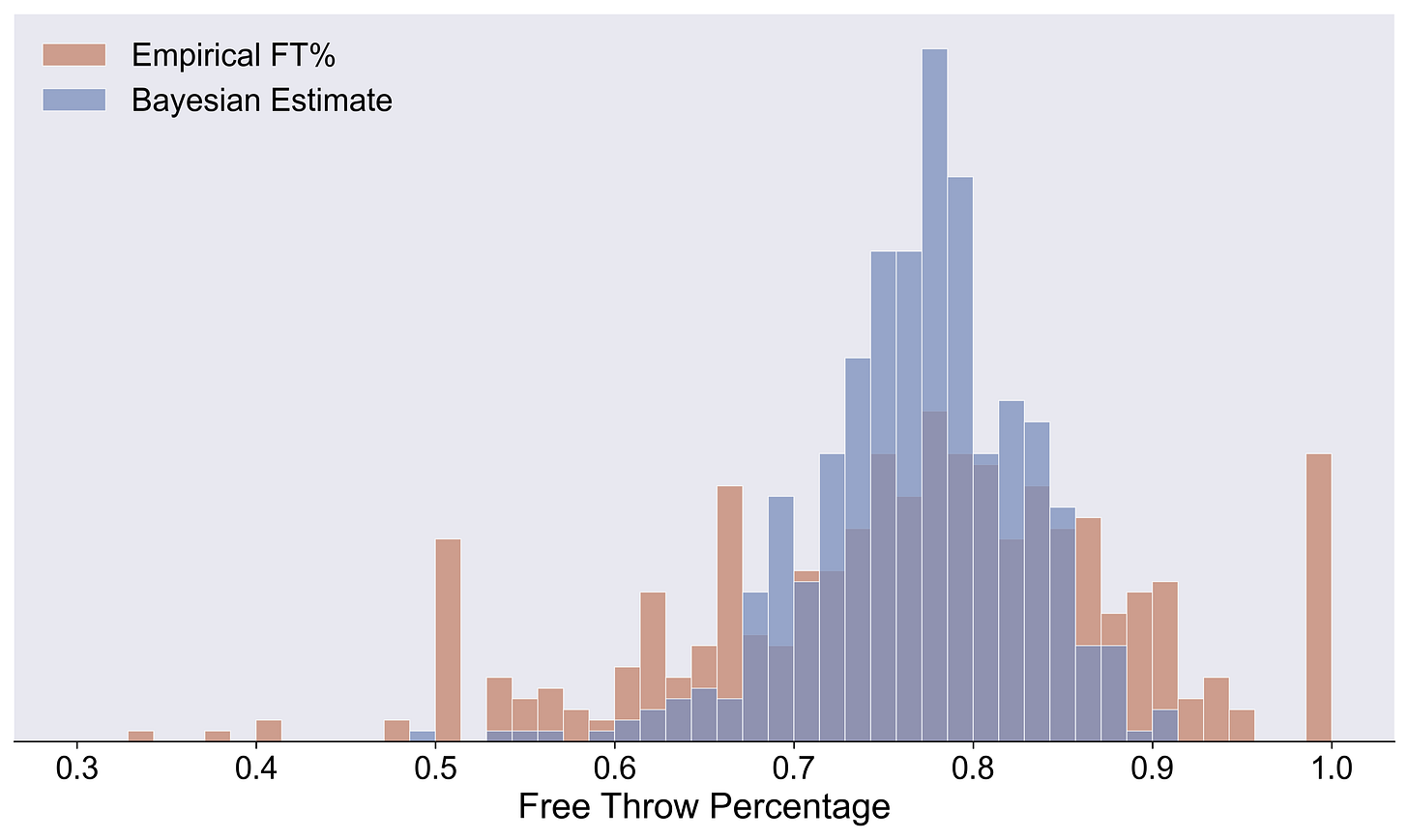
Bayesian free throw estimates vs empirical estimates

Here’s a plot of our bayesian estimates for each player in the league (blue) vs their corresponding empirical estimates (orange).

All those 100% shooters? All the extremes? The model is just saying, there’s no way they’re that good/bad.

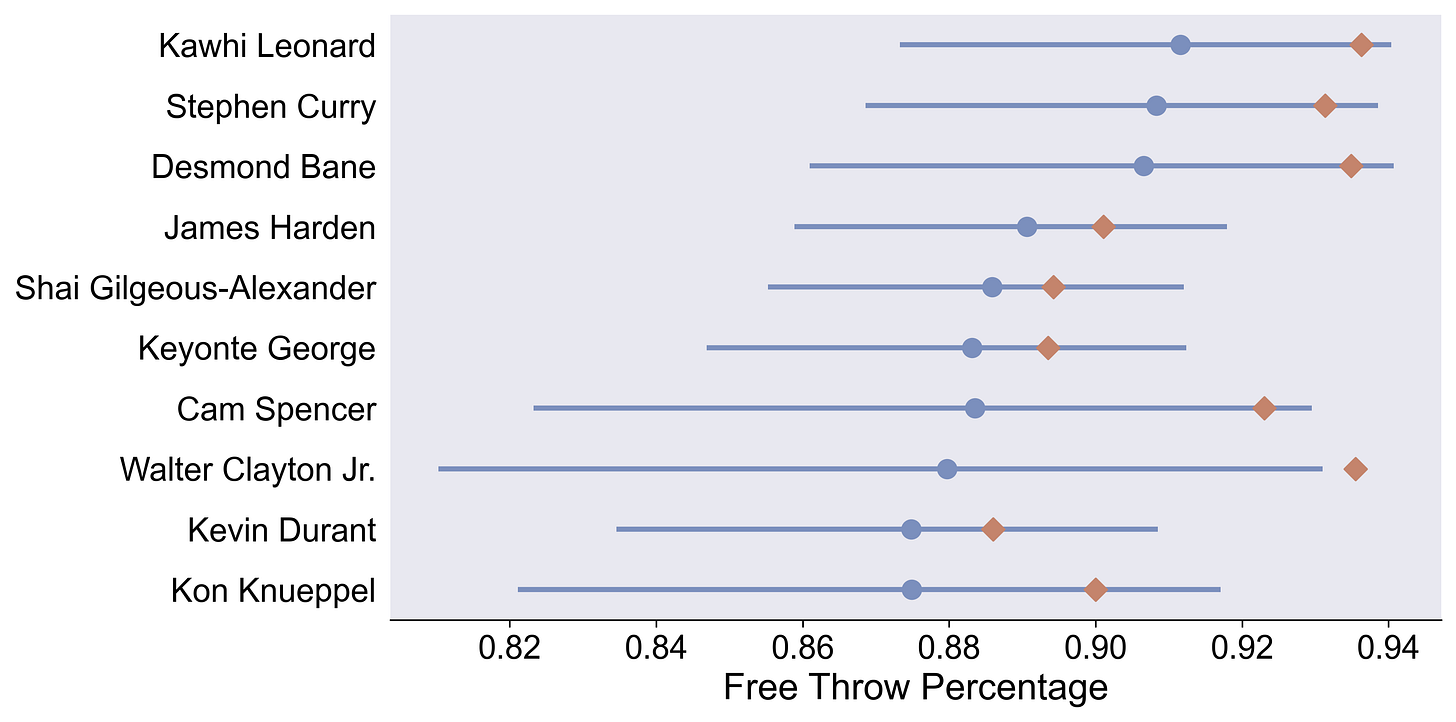
Best Free Throw Shooters

Bayesian (blue) and empirical (orange) free throw percentage estimates per player

Here are the top 10 shooters this season. The blue dot shows the posterior median, compared to their empirical free throw percentage (orange diamond). I think there’s three important things to point out:

1. There’s a lot of uncertainty. To answer the question in the title of this post: I don’t know.

2. The model may be too conservative. Future posts will follow up.

3. Walter Clayton Jr. is empirically very good, but this clearly shows we just haven’t seen enough to know for sure, yet.

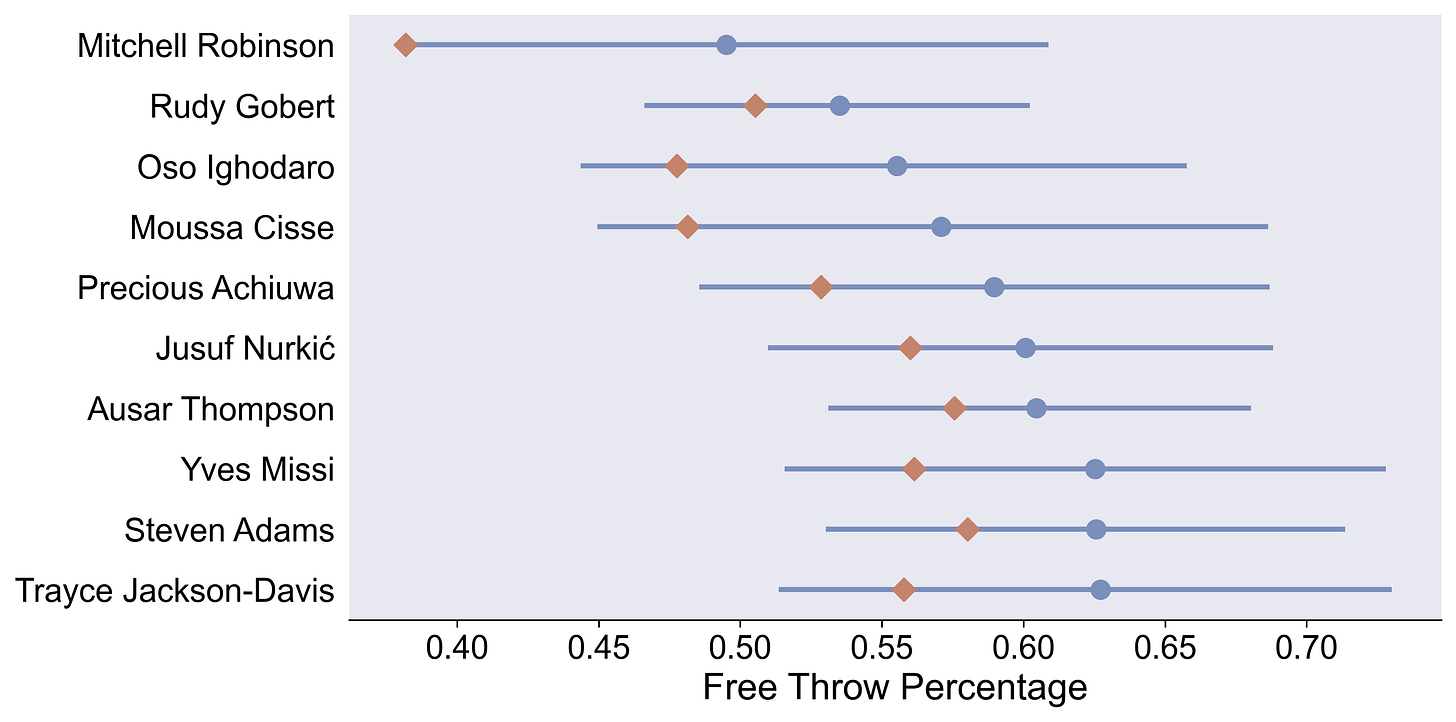
Worst Free Throw Shooters

Bayesian (blue) and empirical (orange) free throw percentage estimates per player

Two notes:

1. The model’s like: No, Mitchell Robinson can’t be that bad.

2. There is so much certainty in how bad Rudy Gobert is.

Looking Ahead

I feel like I’m coming out of a coma. I wanted to start with something simple just to get pen on to paper. In the next post we’ll see what we can do about Kawhi Leonard.

Model

data {
  int<lower=0> N;                 // number of players
  array[N] int<lower=0> fta;      // free throw attempts
  array[N] int<lower=0> ftm;      // free throws made
}

parameters {
  real mu;                        // population mean (logit scale)
  real<lower=0> sigma;            // population sd
  vector[N] theta;                // player-specific ability (logit scale)
}

model {
  // Priors
  mu ~ normal(1.1, 0.5);          // ~75% FT prior on probability scale
  sigma ~ exponential(2);

  // Hierarchical prior for player abilities
  theta ~ normal(mu, sigma);

  // Likelihood
  ftm ~ binomial_logit(fta, theta);

}

generated quantities {
  vector[N] ft_pct;
  ft_pct = inv_logit(theta);      // transform to probability scale
}