Comprehensive NBA 3PT Modeling

Extending our FT modeling to 3PT shooting

Previously, we wrote up our comprehensive FT model.

Comprehensive NBA Free Throw Modeling

Here, we adapt this same model to 3PT shooting.

Model

The full Stan model is at the bottom of this post. At a high level, we’re using a hierarchical binomial model, pooled by player position (guard, forward, center), using the following features:

• Height

• Experience

• Draft Position

• Weight

• International vs US

Remember, as this is hierarchical, when players have few attempts, the model basically shrugs and assumes they are going to look like other players with their features.

Results

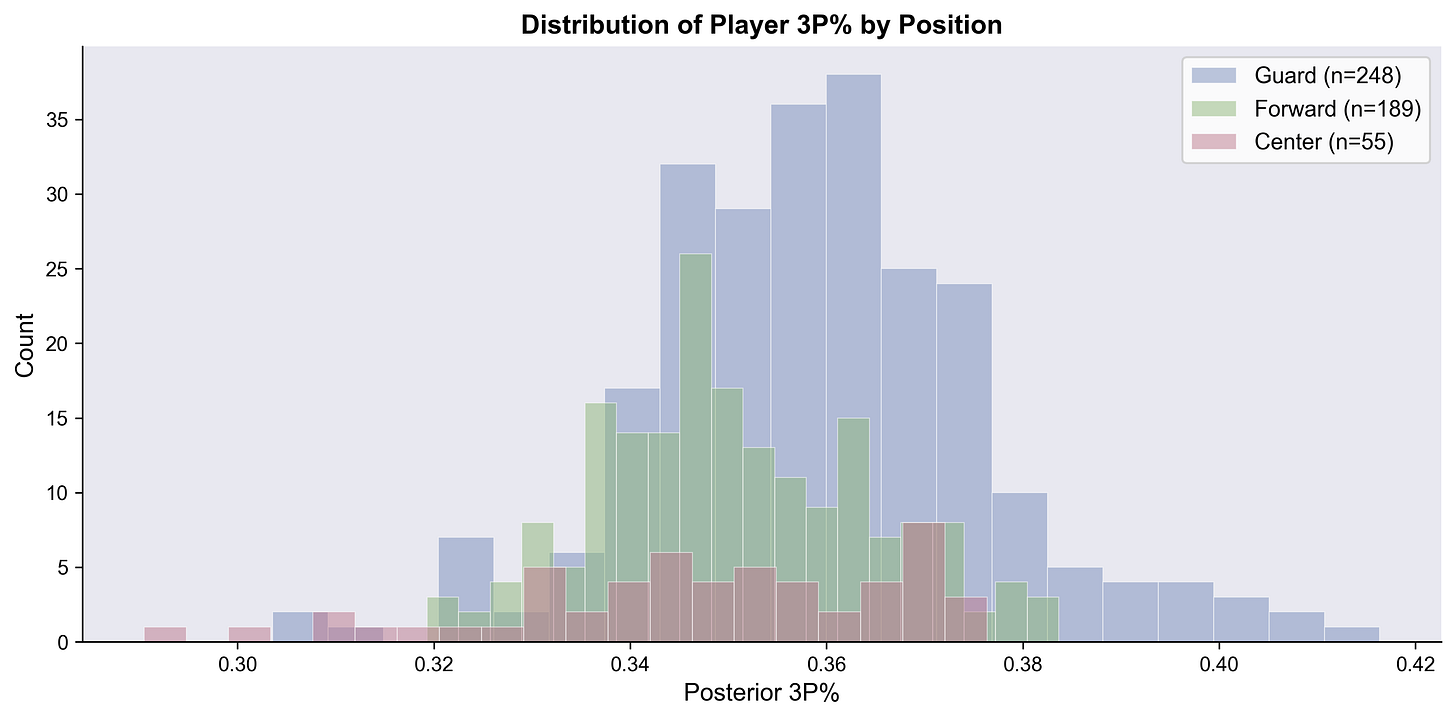
Player Distribution

Here’s the distribution of 3PT% estimates for all players in the league, broken out by position. This distribution is so interesting to me. Tons of variance, which makes sense, but there’s this long-tail shoulder on the guards above 38%.

Now, lets inspect each feature.

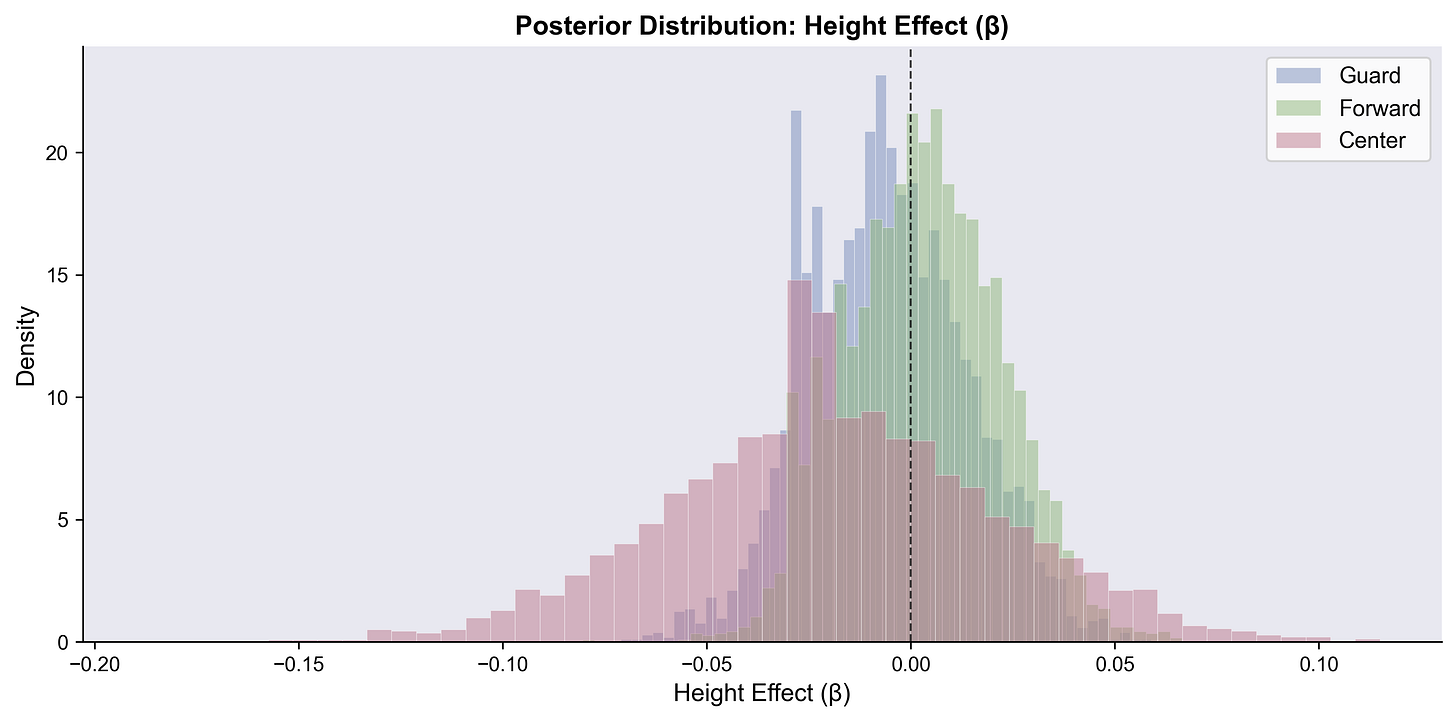
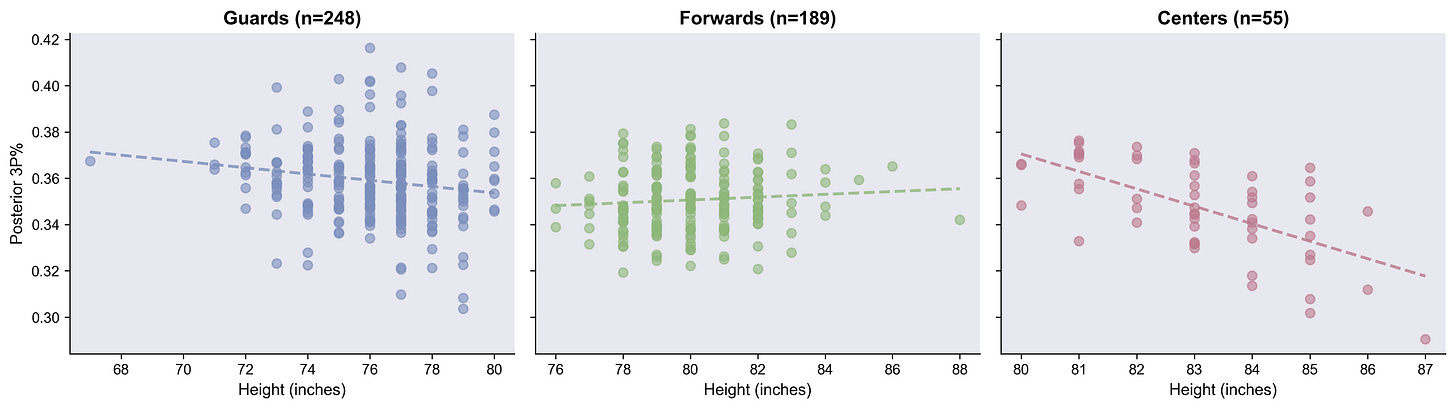
Height: No definitive effect, Taller centers might be affected

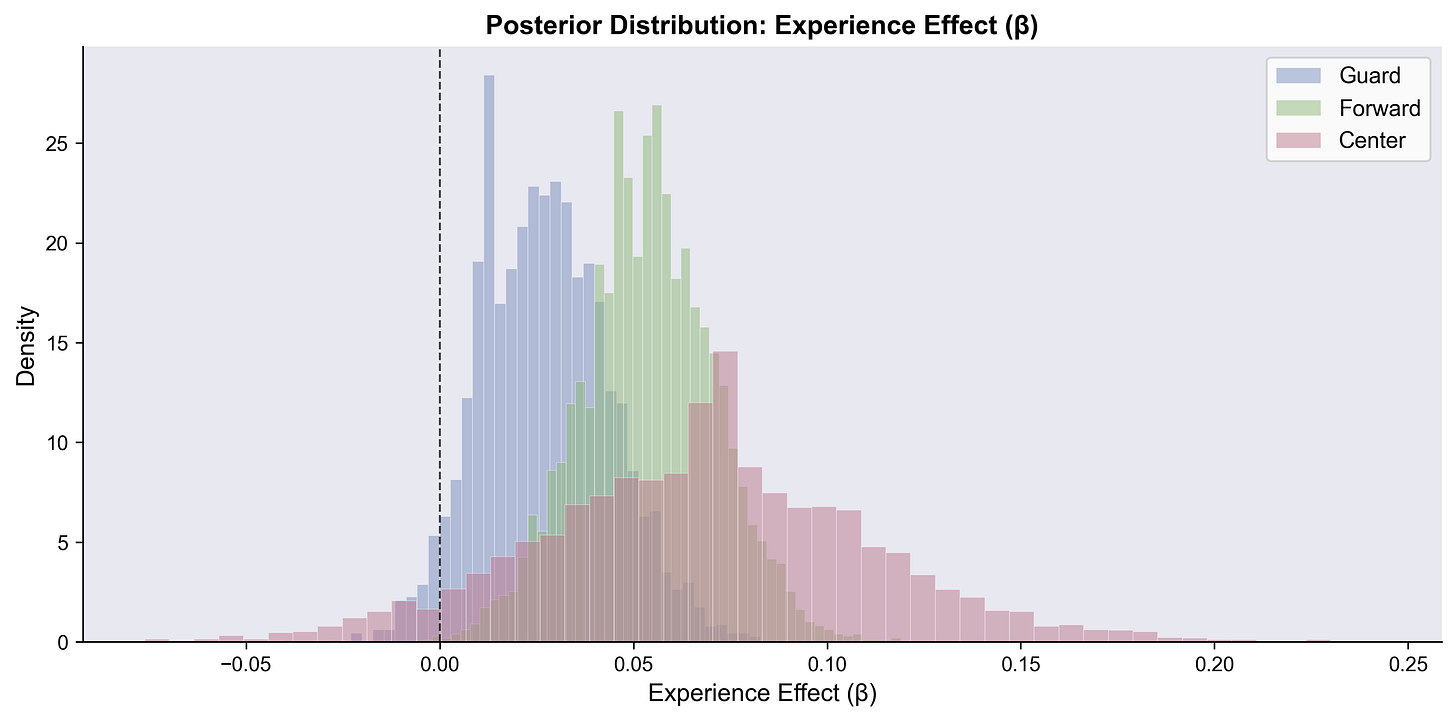
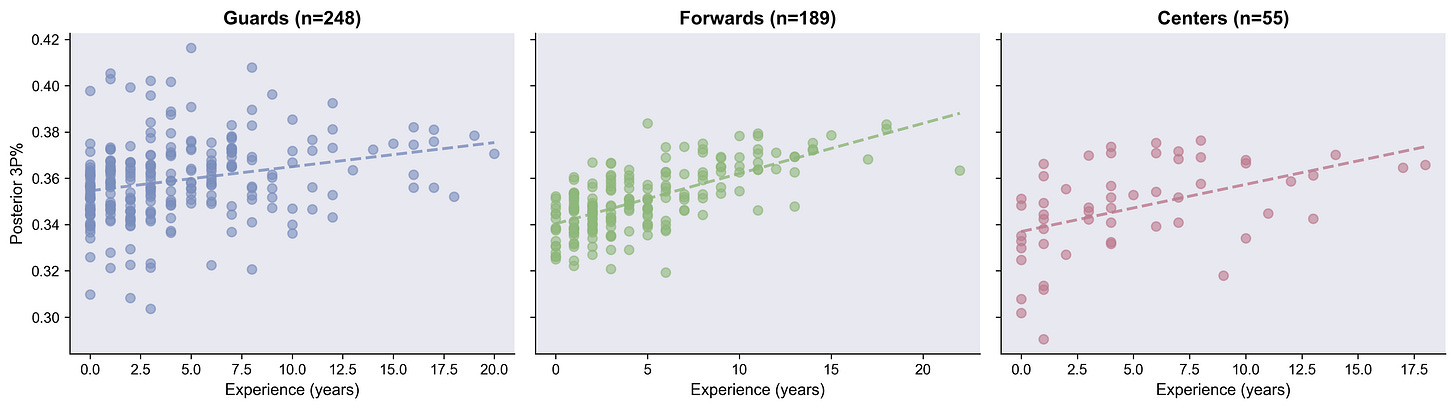
Experience: Obvious effect

Probably survivorship bias, but interesting nonetheless.

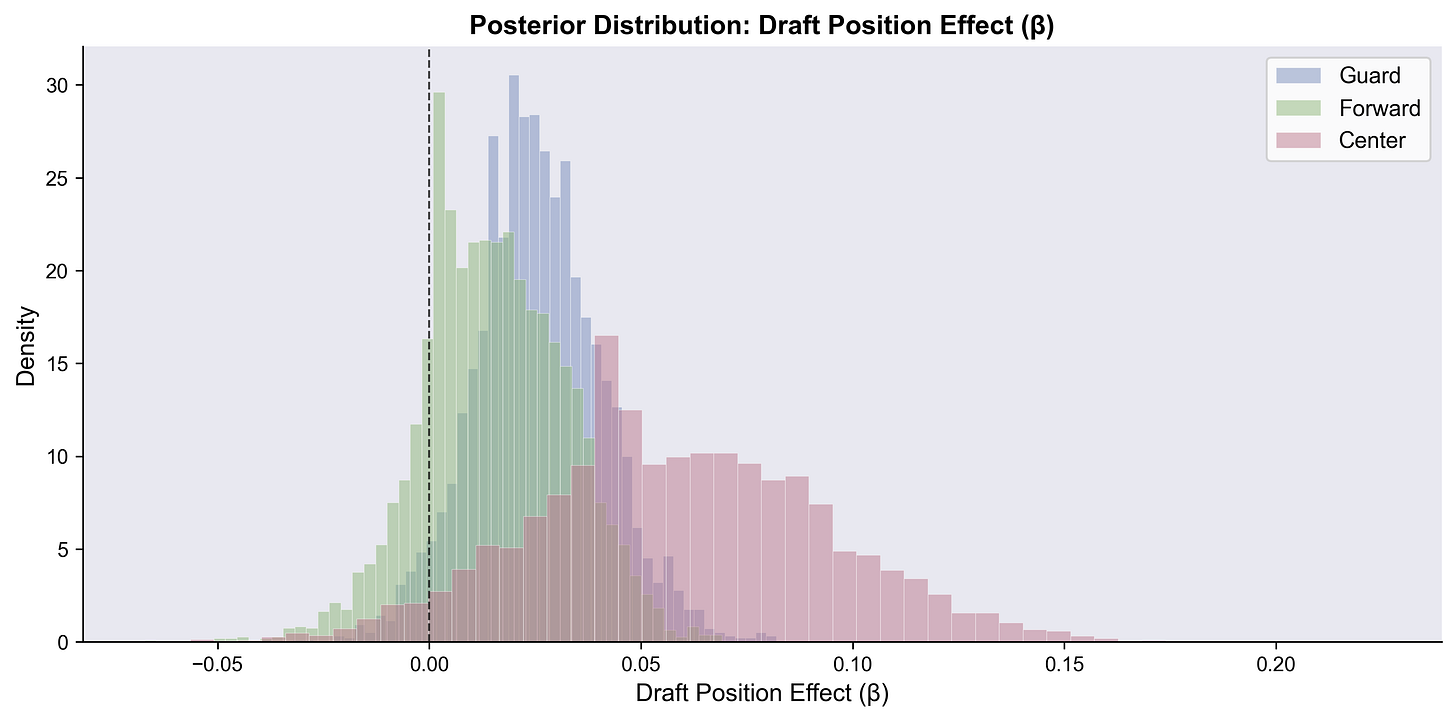
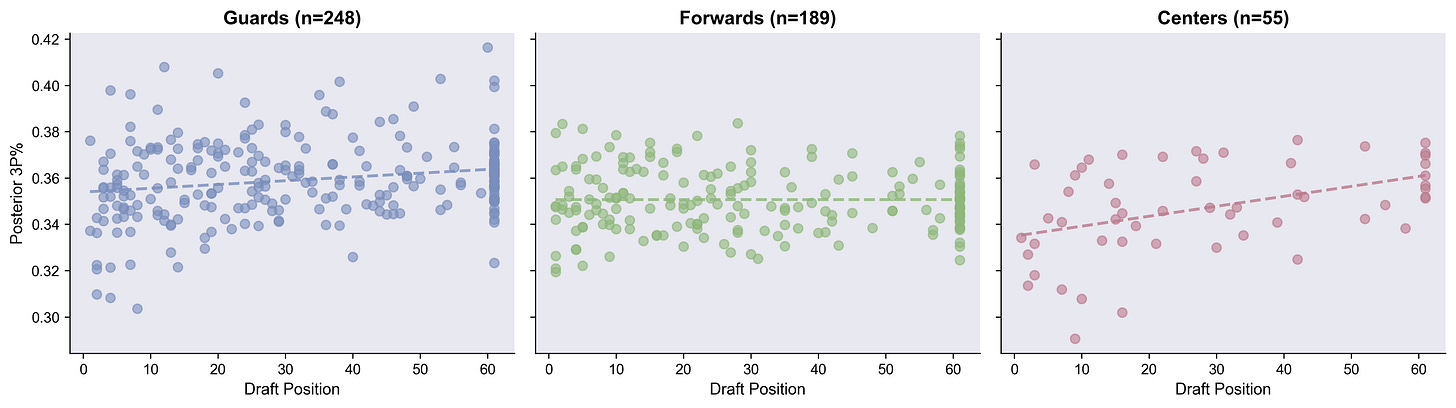
Draft position: Surprising, but makes sense

Later draft positions, especially for big men, predicts higher three point shooting. If you think about the archetype of centers that are drafted early vs later (and who is picked up undrafted), this isn’t as counter-intuitive as it seems. To me, the main question is, why didn’t we see this in our FT modeling.

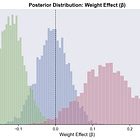
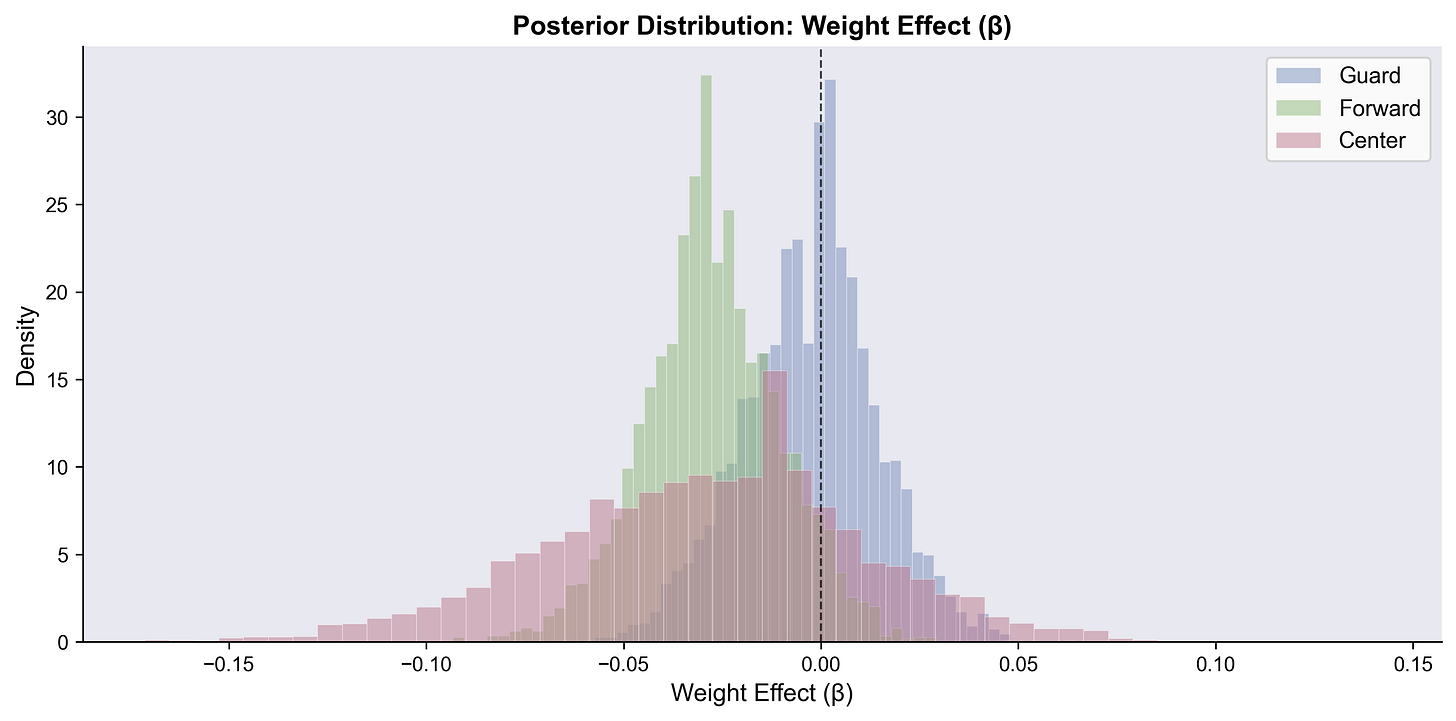
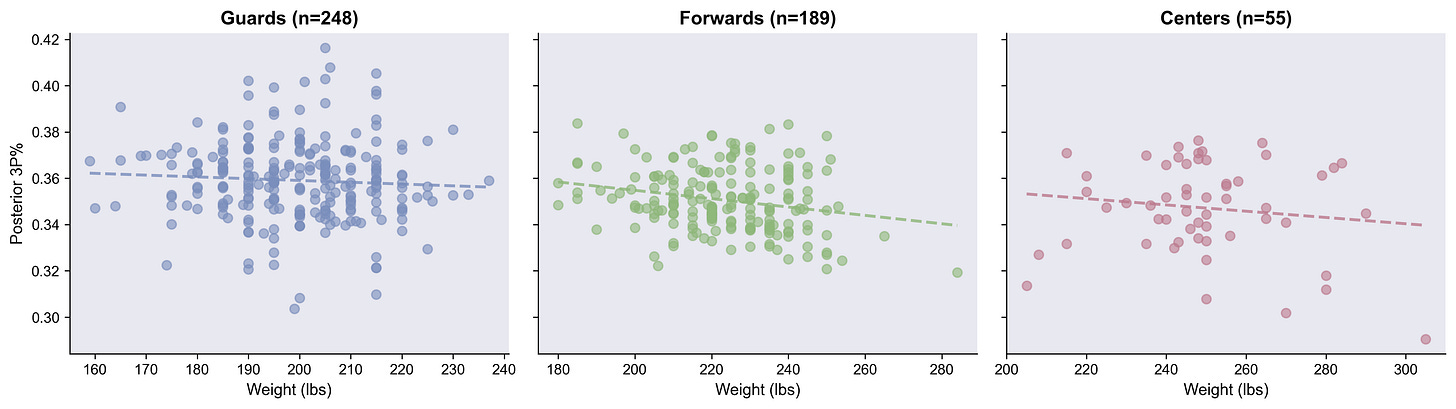
Weight: Nothing to write home about

A lot of density for the Center position’s weight goes negative, which I can buy. Guards, perfectly centered on zero, which also makes sense. Lighter centers might be better at shooting threes, while weight doesn’t affect guards as much.

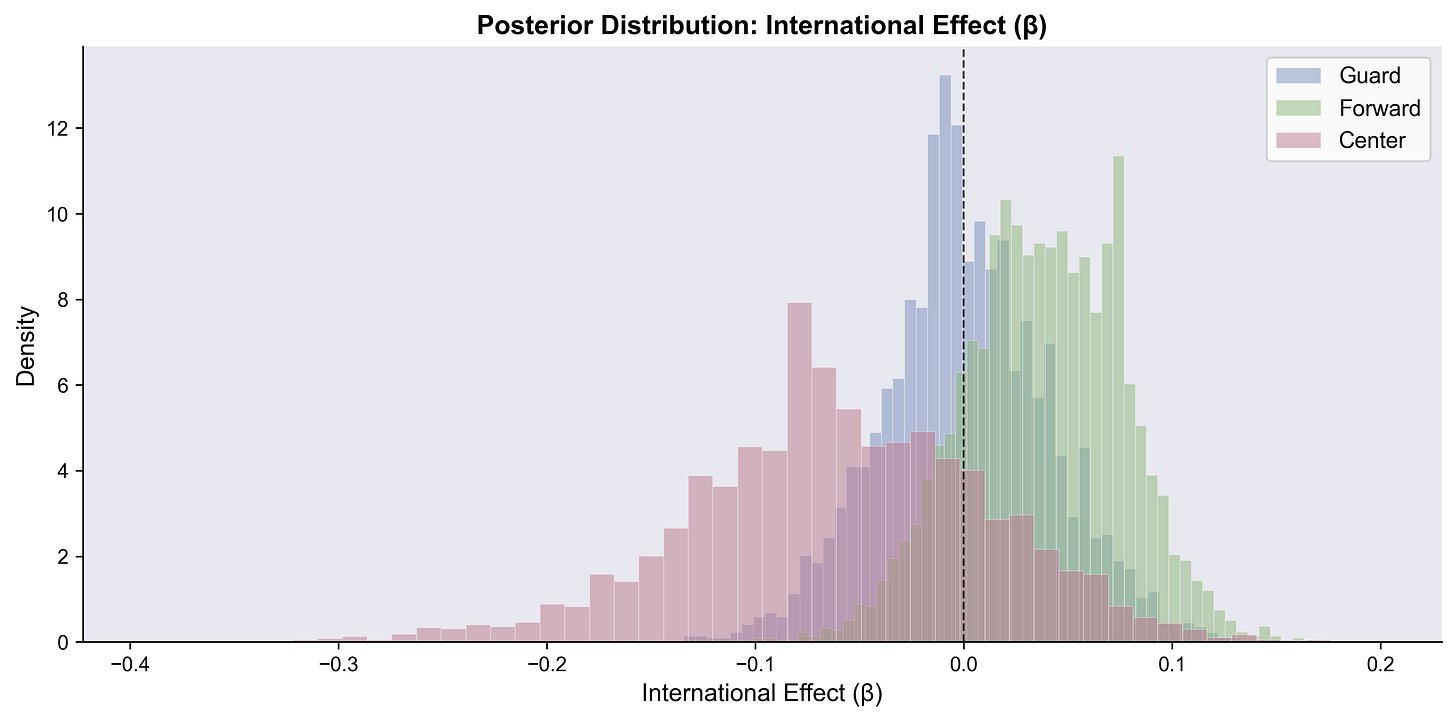
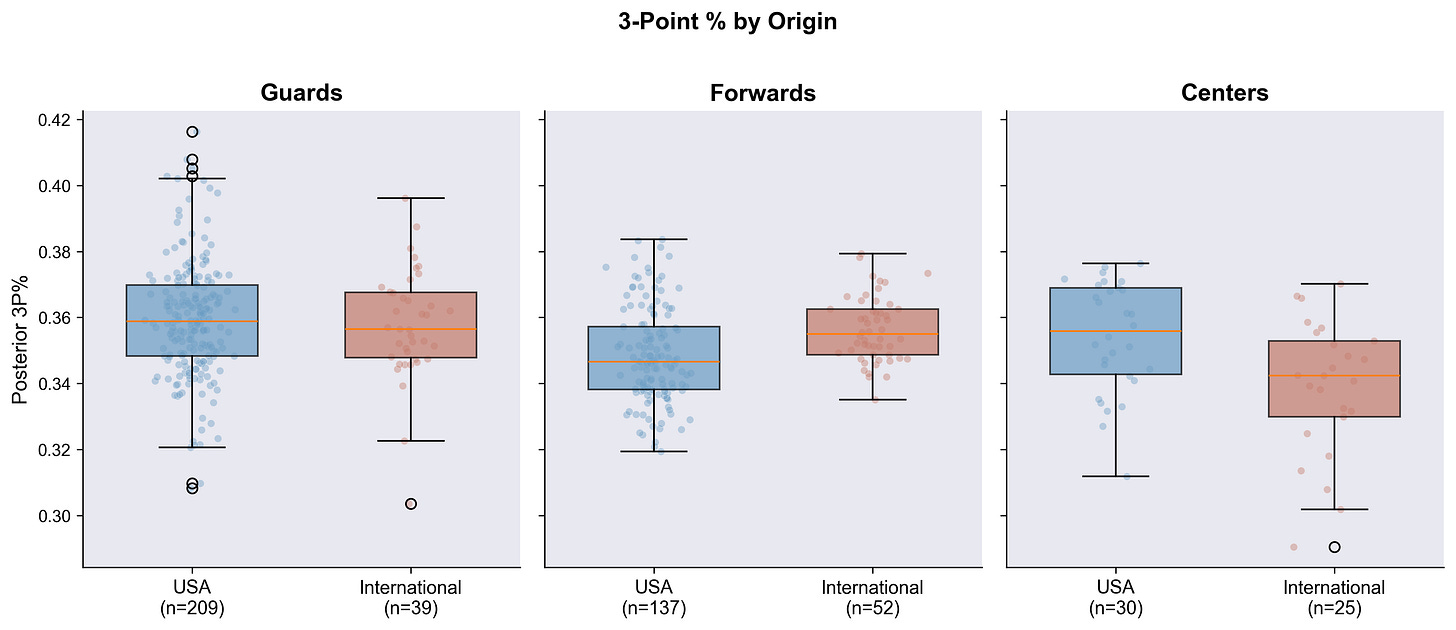
International vs US

Nothing to see here.

Full Stan Model

// Extended hierarchical binomial model for 3-point shooting
// Position-specific coefficients for 5 regressors:
// height, experience, draft position, weight, international

data {
  int<lower=0> N;                 // number of players
  int<lower=1> P;                 // number of positions (3)
  array[N] int<lower=1,upper=P> position;
  array[N] int<lower=0> fg3a;     // CHANGED: fta -> fg3a
  array[N] int<lower=0> fg3m;     // CHANGED: ftm -> fg3m
  
  // Regressors (all standardized)
  vector[N] height_z;
  vector[N] exp_z;
  vector[N] draft_z;
  vector[N] weight_z;
  vector[N] is_intl;              // binary: 0=USA, 1=international
}

parameters {
  vector[P] mu;                   // position intercepts (logit scale)
  
  // Position-specific coefficients
  vector[P] beta_height;
  vector[P] beta_exp;
  vector[P] beta_draft;
  vector[P] beta_weight;
  vector[P] beta_intl;
  
  vector<lower=0>[P] sigma;       // position residual sds
  vector[N] theta;                // player abilities (logit scale)
}

model {
  // Priors on intercepts
  // CHANGED: Centered at -0.5 (approx 38% 3PT) instead of 1.1 (75% FT)
  mu ~ normal(-0.5, 0.5);          
  
  // Priors on coefficients (weakly informative)
  beta_height ~ normal(0, 0.3);
  beta_exp ~ normal(0, 0.3);
  beta_draft ~ normal(0, 0.3);
  beta_weight ~ normal(0, 0.3);
  beta_intl ~ normal(0, 0.3);
  
  sigma ~ exponential(2);
  
  // Player abilities with all regressors
  for (n in 1:N) {
    real linear_pred = mu[position[n]] +
                       beta_height[position[n]] * height_z[n] +
                       beta_exp[position[n]] * exp_z[n] +
                       beta_draft[position[n]] * draft_z[n] +
                       beta_weight[position[n]] * weight_z[n] +
                       beta_intl[position[n]] * is_intl[n];
    theta[n] ~ normal(linear_pred, sigma[position[n]]);
  }
  
  // Likelihood
  fg3m ~ binomial_logit(fg3a, theta);
}

generated quantities {
  vector[N] fg3_pct;
  vector[P] mu_pct;
  
  fg3_pct = inv_logit(theta);
  mu_pct = inv_logit(mu);
}